路遙知碼力，日久練成精-只要在程式之路鑽研的夠深，便能夠充分發揮程式碼的力量; 練習的日子夠久，便能夠練成寫出精簡代碼的能力。

首先先來討論一下昨日課後練習的解答:
(還沒看過題目的朋友歡迎點昨日題目傳送門)

昨日課後練習討論

def trans(article):
    return ''.join([c.lower() if c.isalpha() else ' ' for c in article])

想法就是說先用列表生成式換字，
如果原來是個英文字母就把它變小寫，
其它情況都換成空白，
再用join函數把列表的字元串起來，
即達到去除標點符號的效果了。
若有其它解法也歡迎於留言區討論哦。

方便窮舉排列組合的itertools

今天要來給大家介紹python中一個好用的模組- itertools，
此模組可以方便的產生各種實用的迭代器，
不過在本文我們只針對常用的「排列組合」做介紹。
itertools可以非常方便的幫我們解決排列組合上的問題:
例如我們想從1~5這五個數字中任取2個數來排列，
或是我們想要1~5這五個數字中任取2個數的組合。

排列、組合傻傻分不清?

相信排列組合可能是許多人中學數學的惡夢，
這邊快速幫大家回憶一下，
究竟「排列」與「組合」這兩個詞有什麼區別呢?
「排列」指的是取出元素的順序不同就視為是不同的狀況，
而「組合」指的是我們只在乎取出的是哪幾個元素不在乎順序。
例如說假設我們有「紅球、藍球、白球」三種不同顏色的球，
如果想要取2顆球出來排列，表示
「先取紅球再取藍球」與「先取藍球再取紅球」是不同的情況，
如果只是要取2個球的組合，那麼不論「紅球、藍球」哪個先取都是一樣的。
附上簡單的圖幫助大家記憶: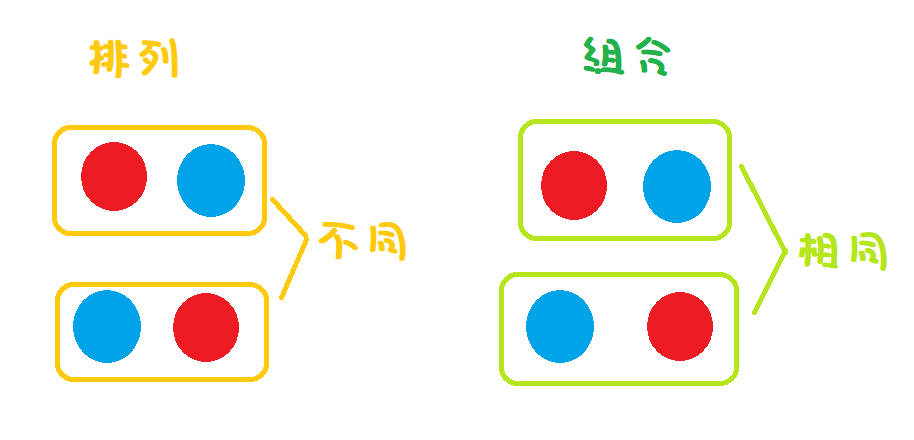

itertools 的使用

透過python內建模組，可以用很短的程式碼來實現排列組合而不必自己實作
首先看程式碼例子:

排列

from itertools import permutations
print(list(permutations("ABCD",2)))

結果為:[('A', 'B'), ('A', 'C'), ('A', 'D'), ('B', 'A'), ('B', 'C'), ('B', 'D'), ('C', 'A'), ('C', 'B'), ('C', 'D'), ('D', 'A'), ('D', 'B'), ('D', 'C')]

組合

from itertools import combinations
print(list(combinations("ABCD",2)))

結果為:[('A', 'B'), ('A', 'C'), ('A', 'D'), ('B', 'C'), ('B', 'D'), ('C', 'D')]

元素可重複的組合

from itertools import combinations_with_replacement
print(list(combinations_with_replacement("ABCD",2)))

結果為:[('A', 'A'), ('A', 'B'), ('A', 'C'), ('A', 'D'), ('B', 'B'), ('B', 'C'), ('B', 'D'), ('C', 'C'), ('C', 'D'), ('D', 'D')]

笛卡兒積

from itertools import product
print(list(product('ABC', 'xyz')))

結果為:[('A', 'x'), ('A', 'y'), ('A', 'z'), ('B', 'x'), ('B', 'y'), ('B', 'z'), ('C', 'x'), ('C', 'y'), ('C', 'z')]
關於這些函數怎用用的詳細語法，
可參考官方文檔或這篇文章的整理，
在本文中就不贅述語法了，
而著重如何運用。
(其中本文特別講「排列」的運用)
首先先上一題「有趣程式問題」吧。

範例26-1 有趣程式問題

此題的題目名稱如標題，
就叫作「有趣程式問題」，
我們有一道乘法算式有趣程式問題 × 程 = 程式問題有趣，
其中每個國字各自對應數字1~9中不同的數字，
你能夠解開這個算式嗎?

這題若是用手算的話，
可能需要還不錯的數學推理能力，
但是既然可以寫程式的話，
我們有個簡單粗暴的方法，
就是窮舉所有數字1~9取六個數字的排列。
然後我們會得到很多元組(比如: (1,2,3,4,5,6))，
再假設它們對應到(有, 趣, 程, 式, 問, 題)這六個字，
一一檢查是否滿足結果，
程式碼如下:

def tupleToNum(Tuple):
    return int(''.join(map(str,Tuple)))
def check(Tuple):
    return tupleToNum(Tuple)*Tuple[2]==tupleToNum(Tuple[2:]+Tuple[:2])
for p in permutations(range(1,10),6):
    if check(p):
        print(p)

結果為(1, 4, 2, 8, 5, 7)。
程式碼可能有點高級，
這邊解說一下每個函數的功能:
tupleToNum函數是將一個元組轉換成數字的形式，
譬如說(1,2,3,4,5,6)轉換為數字123456。
check函數是檢查將數字代入有趣程式問題是否滿足等式。
for迴圈則是窮舉所有排列，若找到解則印出來。
程式幫我們找到唯一的一組解(1, 4, 2, 8, 5, 7)。
我們可以實際按計算機，
發現142857*2=285714。

範例26-2 三分數之和等於1

題目如下，要在a~i九個字母中不重複的填入1~9，
使得三個分數相加的和為1。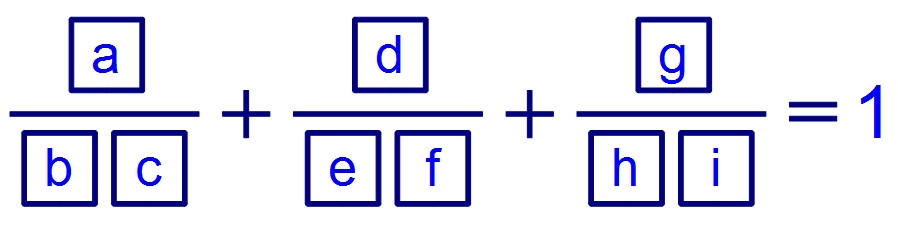

程式如下:

from itertools import permutations

def tupleToFloat(Tuple):
    return Tuple[0]/(Tuple[1]*10+Tuple[2])
def check(Tuple):
    return tupleToFloat(Tuple[0:3])+tupleToFloat(Tuple[3:6])+tupleToFloat(Tuple[6:9])==1
for p in permutations(range(1,10),9):
    if check(p):
        print(p)

解說程式碼意思，
tupleToNum函數是將一個元組轉換成浮點數的形式，
譬如說(1,2,3)轉換為浮點數1/23的結果。
check函數用來檢查每組答案是否滿足等式。
結果為:
(5, 3, 4, 7, 6, 8, 9, 1, 2)
(5, 3, 4, 9, 1, 2, 7, 6, 8)
(7, 6, 8, 5, 3, 4, 9, 1, 2)
(7, 6, 8, 9, 1, 2, 5, 3, 4)
(9, 1, 2, 5, 3, 4, 7, 6, 8)
(9, 1, 2, 7, 6, 8, 5, 3, 4)
得到六組答案。
不過考量到三個分數之間可以互相交換，
答案恰好為一組，
也就是5/34+7/68+9/12=1呢。

課後練習

路遙知碼力系列接近尾聲了呢，
在此之前試試這道題吧。
這裡有一道有趣的直式加法: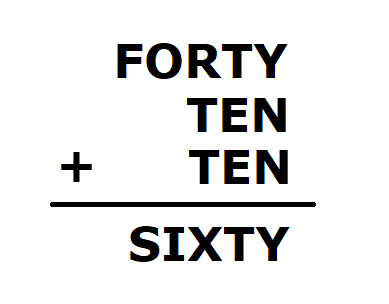

其中(F,O,R,T,Y,E,N,S,I,X)每個字母對應到0~9的不同數字，
你能夠把所有可能解找出來嗎?